מדריך | הקסדצימאלי | צעד נוסף להבנת עולם הנתונים

דאבל

חברים, הפרוייקט מתקדם! טלו חלק במגבית... אה, במדריך, או יותר נכון סדרת המדריכים.
אולי כולם מחפשים את התשובה לשאלה "מה עושים?" ורוצים את התכלס', (וגם זה יגיע בעז"ה) וזה לא עובד ככה! בשביל זה יש את הפורום לשאול "איזו תוכנה הכי טובה?" בלי לזלזל חלילה! אבל המדריכים האלו מיועדים בעיקר למי שרוצה ללמוד, להשקיע, ולהחכים לדעת על מה בכלל אנחנו מדברים (כמובן בצורה פשוטה וברורה) כשנכנסים ל"עולם המידע והנתונים" (לא "השחזור" זה יגיע ממילא...) אז לא חייבים לחכות שאני או @web_master נעלה מדריך חדש, תבחרו נושא בתיאום מראש ותתחילו ללמוד...
זה מה שאני עושה מעת לעת בכ"א...
כאן נמצא "אינדקס הנושאים" לכתיבה.

אז הנה סיימתי עוד פרק, קחו נשימה עמוקה ותקפצו פנימה

ברוכים הבאים לעולם המספרים ההקסדצימאליים:

הקסדצימאלי - שפה סודית של מחשבים?
תארו לעצמכם שוב את מחסן הלבנים שלנו. זוכרים? המחסן מלא בלבנים בודדות, חסרות משמעות כמעט, שהן כמו ביטים בודדים - 0 ו-1.
כדי לעבוד עם כמויות גדולות של ביטים בצורה יותר נוחה ויעילה, אנחנו מקבצים אותם לקבוצות. כבר פגשנו את ה בייט - קבוצה של 8 ביטים. בייט הוא כמו מילה קצרה בעולם הבינארי. והיא השימושית מבין כולם לאדם אנושי. (מילה היא לא הדוגמה הנכונה
אם אנחנו רוצים לדייק, הנה פירוט קצר על קבוצות שונות של ביטים:
ניבל (Nibble): 4 ביטים. Word: תואם למעבד- כיום 64 ביט, (תלוי במחשב - כמובן רוב המחשבים היום הם 64...)
ויש את Quad Word או Double Word שרלוונטיים בעיקר במחשבים עם ארכיטקטורה 86x)

אבל לפעמים, גם בייטים בודדים עדיין יכולים להיות מסורבלים לקריאה ולכתיבה, במיוחד כשמדובר ברצפים ארוכים של בייטים, כמו כתובות זיכרון, קודי צבע, או נתונים בינאריים גולמיים.
כאן נכנס לתמונה ההקסדצימאלי, הוא כמו שפה מקוצרת, קוד סודי שמאפשר לנו לייצג רצפים ארוכים של ביטים בצורה יותר קצרה וקריאה יחסית לבני אדם.

הצורך בהקסדצימאלי:
תארו לעצמכם שאתם צריכים לרשום מספר טלפון ארוך מאוד - נגיד מספר טלפון בינלאומי עם קידומת ארוכה. לכתוב את כל הספרות אחת אחרי השנייה יכול להיות ארוך ומייגע, וגם קשה לזכור ולבדוק אם העתקתם נכון.
מה כולנו עושים כדי לפשט את זה? אנחנו מקבצים את הספרות לקבוצות קטנות, למשל קבוצות של 3 או 4 ספרות, ומוסיפים רווחים או מקפים בין הקבוצות. זה עוזר לנו לקרוא ולזכור את המספר יותר בקלות, ולזהות שגיאות אם יש.
הקסדצימאלי עושה משהו דומה, אבל הוא מקבץ ביטים לקבוצות של 4 ביטים בכל פעם.

למה דווקא 4 ביטים?
כי קבוצה של 4 ביטים יכולה לייצג בדיוק 16 ערכים שונים (מ-0000 בינארי עד 1111 בינארי). וזה בדיוק מספר הספרות שיש לנו בשיטה ההקסדצימאלית!
וזה הקשר המיוחד בין בינארי להקסדצימאלי, 2 בחזקת 4 =16!

הכרת הספרות ההקסדצימאליות - לא רק מספרים!
בשיטה העשרונית הרגילה (דצימלית), יש לנו 10 ספרות: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
(יש עוד סוגים של בסיסי ספירה, אבל לא רלוונטיים אלינו...)
הקסדצימאלי (בסיס 16) זה פשוט שיטה מגניבה לספור, כמו עשרוני שאנחנו רגילים, רק קצת אחרת. בעשרוני יש לנו 10 ספרות (0 עד 9), נכון? אז בהקסדצימאלי יש לנו... ניחשת נכון! 16 "ספרות". אבל רגע, אין לנו מספיק ספרות רגילות! אז מה עושים?
מכירים את החברים החדשים - A, B, C, D, E, F!
במקום להמשיך עם 10, 11, 12 וכו', בהקסדצימאלי אנחנו משתמשים באותיות! זה נשמע מוזר, אבל זה ממש פשוט:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 - אלה כרגיל, אין הפתעות.
A - זה כמו 10 בעשרוני.
B - זה כמו 11 בעשרוני.
C - זה כמו 12 בעשרוני.
D - זה כמו 13 בעשרוני.
E - זה כמו 14 בעשרוני.
F - זה כמו 15 בעשרוני.
חשוב! אחרי F, אנחנו לא עוברים ל-G, אלא, אחרי F מגיע... 10!
כן, בדיוק כמו בעשרוני, אחרי 9 מגיע 10, בהקסדצימאלי אחרי F מגיע 10. זה אומר ש-'10' בהקסדצימאלי זה כבר המספר 16 בעשרוני! קצת מוזר בהתחלה, אבל תתרגל.

רשימת הסימנים בשיטה ההקסדצימאלית עם הערך שלהם (שהוא גם זהה לערך העשרוני):
0 = 0
1 = 1
2 = 2
3 = 3
4 = 4
5 = 5
6 = 6
7 = 7
8 = 8
9 = 9
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15

(חשוב לזכור להמשך: הסימן 'F' בהקסדצימלי מייצג את הערך העשרוני 15, ולא 16.)
האמת שזה דווקא נחמד הקטע עם האותיות, יכול להיות צירופי מספרים שירכיבו מילים באנגלית... אבל אנחנו לא נתבלבל בין מספרים הקסדצימליים למילים, אל דאגה. (כבר נסביר איך אנחנו מזהים אותם...)

העיקרון הבסיסי ברור, עכשיו בואו נתקדם קצת.

ערך המיקום:
במספרים עשרוניים שאנחנו רגילים אליהם, יש חלוקה לרמות בחזקה של 10 ככה שהערך של המספר גדל ככל שהוא נמצא שמאלה
חזקה היא דרך קצרה לכתוב פעולת כפל של מספר בעצמו מספר מסוים של פעמים.

(כעיקרון כשאנחנו מסתכלים על ספרה בודדת, אין מה להסתבך, פשוט מסתכלים בטבלה אם לא זוכרים בעל-פה את הערכים ההקסדצימאליים, בשתי ספרות ומעלה: כאן נכנס לתמונה העניין של בסיס 16 והחזקות שלו. כל מיקום של ספרה מייצג חזקה של 16. לכן, כדי להבין את הערך העשרוני של מספר הקסדצימאלי עם שתי ספרות או יותר, אנחנו חייבים לבצע את ההמרה לפי המיקום והערך של כל ספרה.)

המרת מספרים הקסדצימאליים לעשרוניים:
בשיטה ההקסדצימלית, כמו בשיטה העשרונית, למיקום של כל סימן במספר יש ערך. הערך של כל מקום גדל בחזקות של 16 ככל שזזים שמאלה:

נבין את זה לאט לאט.

ניקח את המספר 11 ונפרק אותו מימין לשמאל:
1 נמצא במקום של היחידות, הערך שלו הוא 1, פשוט.
ה-1 השמאלי נמצא במקום של "העשרות" שזה 16 בהקס, הערך שלו הוא 16.
התוצאה היא 17.
'10': האפס פה "שומר מקום" ליחידות, ומוודא שה-'1' יהיה במקום של ה-16. בלי האפס, זה היה סתם '1', שזה רק 1 כמו גם בעשרוני.

(נזכור שהערך של 0 תמיד 0: הספרה '0' בהקסדצימלי תמיד מייצגת את הערך העשרוני 0, ללא קשר למיקום שלה.)

ניקח דוגמה נוספת:
המרת FF הקסדצימלי לעשרוני
F (ימני) = 15, 15 * 1 = 15
F (שמאלי) = 15, 15 * 16 = 240
סיכום: 15 + 240 = 255 עשרוני
אנחנו עושים 15 כפול 16 כי הערך של הF הוא 15 אבל הוא נמצא במקום של 16

בוא נהיה ברורים: הכלל להמרה לערך העשרוני הוא, המספר כפול 16 בחזקת המקום שלו בסדר הבא:
0 – 1 – 2 – 3 וכן הלאה.
ה 0 הוא האחדות, כמו שלמדנו, אין מה להמיר בו, הוא שווה לערך שלו,
ה 1 הוא המספר כפול 16 (אם זה 1 הקס, אז זה פשוט 16 עשרוני) בחזקת 1 (שזה אותו דבר בעצם).
ה 2 הוא המספר כפול 16 בחזקת 2 (או אם תרצו המספר כפול 16 כפול 16...)
וכן הלאה...

הכי קל ללמוד בדוגמאות, אז נמשיך:
המרת A0 הקסדצימלי לעשרוני
0 (ימני) = 0, אנחנו מחשבים 0 * 1 = 0
A (שמאלי) = 10, אנחנו מחשבים 10 * 16 = 160
סיכום: 0 + 160 160 = עשרוני

המרת 121 הקסדצימלי לעשרוני
1 (ימני) = 1, 1 * 1 = 1
2 (אמצעי) = 2, 2 * 16 = 32
1 (שמאלי) = 1, 1 * 256 = 256
סיכום: 1 + 32 + 256 289 = עשרוני

המרת 2B3 הקסדצימלי לעשרוני:
3 (ימני) = הערך הקסדצימלי שלו הוא 3, מחשבים: 3 * 1 = 3
B (אמצעי) = הערך הקסדצימלי שלו הוא 11, מחשבים: 11 * 16 = 176
2 (שמאלי) = הערך הקסדצימלי שלו הוא 2, מחשבים: 2 * 256 = 512
סיכום: 3 + 176 + 512 = 691 עשרוני

וכן על זו הדרך:
'100' הקסדצימלי הוא 256 עשרוני: (1 * 1 62) + (0 *1 61) + (0 *1 60) = 256.
'AA' הקסדצימלי הוא 170 עשרוני: (10 * 16) + 10 = 170.

'20' בהקסדצימלי הוא 32 בעשרוני
ה-'0' הימני הוא במקום של 1 60 (יחידות), ערכו 0.
ה-'2' השמאלי הוא במקום של 1 61 (שש-עשרה), ערכו 2.
חישוב: (2) כפול (16) + (0) כפול (1) = 32 + 0 = 32 בעשרוני.

תרגילים (לא להתבלבל!): כמה זה 16 בהקסדצימאלי? ו17? 18ו?
עניתם? אז כמה זה 10? 11? 13? אם לא טעיתם, אז אתם על הגל!

בואו נסכם את הקטע עם המקומות:
המקום הכי ימני (ראשון) - כפול 1.
המקום השני (משמאל) - כפול 16.
המקום השלישי (משמאל) - כפול 16 * 16 (שזה 256).
המקום הרביעי (משמאל) - כפול 16 * 16 * 16 (שזה 4096).
וכן הלאה...

טוב, נראה לי שעד כאן הכל ברור, תבדקו את עצמכם...

מתקדמים, איך ממירים הפוך, עשרוני להקסדצימאלי? נתחיל בדוגמה:

המרת המספר העשרוני 30 להקסדצימאלי:

30 חלקי 16 = 1 עם שארית 14. (14 בעשרוני זה E בהקסדצימאלי)
המנה היא 1, שהיא לא 0, אז ממשיכים.
1 חלקי 16 = 0 עם שארית 1.
המנה היא 0, סיימנו.
השאריות הן 14 (E) ואז 1. בסדר הפוך הן 1E.
לכן, 30 בעשרוני שווה ל- 1 E בהקסדצימאלי.
כלומר אנחנו נחלק את המספר ב 16 נרשום את השארית ואת התוצאה נחלק שוב ב16, ונרשום את השארית
שימו לב שעכשיו המספרים מ 15 ומטה מתורגמים לערך שלהם בהקס, כולל אם השארית היא 0
כעת נחבר הפוך בסדר הפעולות שלנו את השאריות ונקבל את המספר ההקסדצימאלי. מובן? נדגים שוב:

נמיר את המספר העשרוני 4097 להקסדצימאלי:

4097 חלקי 16 = 256 עם שארית 1.
256 חלקי 16 = 16 עם שארית 0.
16 חלקי 16 = 1 עם שארית 0.
1 חלקי 16 = 0 עם שארית 1.
התוצאה האחרונה היא 0, אז אנחנו עוצרים. השאריות שקיבלנו הן 1, 0, 0, 1.
כשנחבר אותן בסדר הפוך, נקבל 1001. (טוב, זה יצא אותו דבר במקרה הזה...)
לכן, 4097 בעשרוני שווה ל-1001 בהקסדצימאלי
אנחנו רואים כאן את העיקרון של הפעולה, אנחנו צריכים להגיע למספר שלא מתחלק ב16 ואז התוצאה היא 0 (אין חצאים, כן?) גם אם נצטרך לחזור על החילוק ב 16 שוב ושוב.

עוד דוגמה, נמיר את המספר העשרוני 48 להקסדצימאלי:

48 חלקי 16 = 3 עם שארית 0.
התוצאה היא 3, שהיא לא 0, אז ממשיכים.
3 חלקי 16 = 0 עם שארית 3.
התוצאה היא 0, סיימנו.
השאריות הן 0 ואז 3. בסדר הפוך הן 30.
לכן, 48 בעשרוני שווה ל-30 בהקסדצימאלי.

יופי! אז עד כאן תיאוריה, בואו נעבור לעולם המעשי יותר, אם אפשר לקרא לזה ככה...

שימושים נפוצים של הקסדצימאלי:
אז איך אנחנו מזהים מספר הקסדצימאלי כשאנחנו פוגשים אותו? יש כמה אופציות, תלוי איפה פגשתם אותו.
1. קידומת של 0x בתחילת המספר. (נכון אתם מכירים? למי לא היה מסך כחול והפנו אותנו להסתכל מה מספר השגיאה...)
2. הספרה 16 בקטן אחרי המספר. לפעמים ככה יכתבו לכם אותו במדריכים שונים, מהיום יהיה לכם קל יותר להתמצאות...
3. האות h אחרי המספר. (ותזהרו לשאול אותי איך לא חושבים שזה חלק מהאותיות של המספר.... ) אבל שימו לב, אם המספר מתחיל בספרה ולא באות צריך להוסיף 0 לפני המספר (אתם מבינים לבד בטח שאין לזה משמעות גם בכל מספר שהוא, כי זה 0 בכל מקרה... כן?)
4. גם "#" בסוף מזהה את המספר כהקסדצימאלי כבר נביא דוגמאות....
(השימושים העיקריים הם 0x בתכנות ו# בייצוג צבעים)
זה חשוב, אם למשל נכתוב 0101 זה יהיה 9 בבינארי. (מה? לא עברתם על המדריך של @web_master רוצו מהר לשם!)
איפה אנחנו פוגשים את ההקסדצימאלי? איפה לא...
בשפות תכנות. כמו פייתון, ג'אווה וכו' שם אנחנו כותבים עם קידומת 0x בד"כ.
אם נכתוב לדוגמא בפייתון:

number = 0xBEA
print(number)

פייתון יבין ש-xBEA0 זה מספר בהקסדצימאלי, והוא ימיר אותו לערך המספרי הדצימלי 3050.
ציון כתובות זיכרון. כתובות זיכרון לרוב מוצגות בהקסדצימאלי. כתובת כמו 0x00401000 מציינת מיקום ספציפי בזיכרון המחשב. (לא לטעות, השגיאה במסך הכחול בווינדוס היא בספרות הקסדצימאליות, אבל לא מצביעה על מיקום בזיכרון, אלא על סוג וחומרת השגיאה.)
ייצוג צבעים בעולם הדיגיטלי. המבנה הוא RGB"" ונכתב כך: RRGGBB# (אדום, ירוק, כחול.) ולכל צבע אפשר לתת ערך בין 0 ל 255:
למשל צבע אדום מלא יהיה FF0000#
#00FF00 - ירוק טהור (מקסימום ירוק, בלי אדום וכחול)
#0000FF - כחול טהור (מקסימום כחול, בלי אדום וירוק)
#FFFFFF - לבן (כל הצבעים מעורבבים בעוצמה מקסימלית)
#000000 - שחור (מינימום אדום, ירוק וכחול - אין אור בכלל)
#808080 - אפור (עוצמה בינונית של כל הצבעים)
#FFA500 - כתום (שילוב של אדום וירוק)
צהוב - #FFFF00 (אדום וירוק מלאים)
נתוני קובץ: כאשר בודקים קובץ בינארי גולמי בתוכנה הקסדצימאלית (Hex Editor), רואים רצף של ערכים הקסדצימאליים. כל זוג ספרות הקסדצימאליות מייצג בייט אחד מהקובץ.(את זה אתם אמורים לדעת כבר, נו, נראה אתכם, למה כל זוג זה בייט?)
אבל לא נעמיק בזה לעת עתה, יהיה לזה פרק במיוחד בעז"ה, ...

אני חושב שאנחנו מוכנים להמשיך הלאה, הקסדצימאלי ובינארי:
טוב, אז כנספח או המשך למדריך על בינארי, בואו נלמד להמיר הקסדצימאלי לבינארי ולהפך: זה כבר חיים קלים,
למה? כי זה באמת קל מאוד! פשוט מקבצים את הביטים בקבוצות של 4, ומתרגמים כל קבוצה לספרה הקסדצימאלית המתאימה.
למשל, נניח שיש לנו את רצף הביטים הבא:
1011010011101010(בינארי)
נחלק לקבוצות של 4 ביטים, מימין לשמאל:
1011 0100 1110 1010
נתרגם כל קבוצה לספרה הקסדצימאלית:
1011 בינארי = B הקסדצימאלי
0100 בינארי = 4 הקסדצימאלי
1110 בינארי = E הקסדצימאלי
1010 בינארי = A הקסדצימאלי
נחבר את הספרות ההקסדצימאליות יחד:
BEA
אז, 1011010011101010 בינארי = BEA הקסדצימאלי.

כדי להמיר מהקסדצימאלי לבינארי, עושים בדיוק הפוך:
לוקחים כל ספרה הקסדצימאלית בנפרד.
מתרגמים כל ספרה לקבוצת 4 הביטים הבינארית המתאימה.
מחברים את קבוצות הביטים יחד.
למשל, נניח שיש לנו את המספר ההקסדצימאלי 2F5:
מפרידים לספרות בודדות: 2 F 5
מתרגמים כל ספרה ל-4 ביטים בינאריים:
2 הקסדצימאלי = 0010 בינארי
F הקסדצימאלי = 1111 בינארי
5 הקסדצימאלי = 0101 בינארי
מחברים את קבוצות הביטים יחד:
0010 1111 0101
אז, 2F5 הקסדצימאלי = 001011110101 בינארי.
להזכירכם, יש לנו כבר טבלה מסודרת של ערכי הבינארי ויש לנו גם טבלה מסודרת של ערכי ההקסדצימאלי! פשוט לחבר אותם יחד!...

החלק הכי טוב בהמרה מהקסדצימלי לבינארי זה שיש לנו טבלה קטנה וסופר קלה לזכור! כל מה שצריך זה לדעת איך כל סימן הקסדצימלי הופך ל-4 ביטים בינאריים: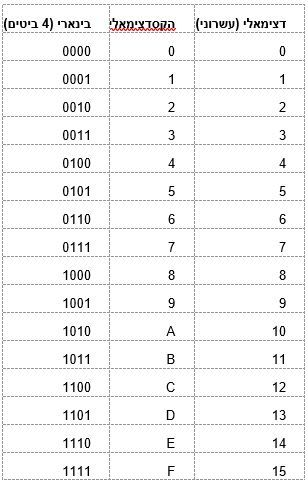

שים לב: כל הערכים הבינאריים בטבלה הם תמיד 4 ביטים (4 ספרות). גם אם המספר קטן, אנחנו מוסיפים אפסים משמאל כדי שיהיו 4 ביטים. למשל, 1 זה לא סתם '1' בינארי, אלא '0001'.
ההמרה הכי קלה בעולם! לוקחים כל סימן במספר ההקסדצימלי, והופכים אותו ל-4 ביטים בינאריים לפי הטבלה! זהו! אין יותר מזה.

כהרגלנו, הכי פשוט ללמוד עם דוגמאות:
המרה של 'F' הקסדצימלי לבינארי:
פשוט הולכים לטבלה, מוצאים את 'F', ורואים שהוא הופך ל-'1111' בינארי.
אז 'F' הקסדצימלי = 1111 בינארי.
המרה של '25' הקסדצימלי לבינארי:
לוקחים כל סימן בנפרד:
'2' הופך ל-'0010' (לפי הטבלה).
'5' הופך ל-'0101' (לפי הטבלה).
מחברים אותם אחד ליד השני: 00100101 בינארי.
אז '25' הקסדצימלי = 00100101 בינארי.

המרה של 'A0' הקסדצימלי לבינארי:
'A' הופך ל-'1010'.
'0' הופך ל-'0000'.
מחברים: 10100000 בינארי.
אז 'A0' הקסדצימלי = 10100000 בינארי.
המרה של '12F' הקסדצימלי לבינארי:
'1' הופך ל-'0001'.
'2' הופך ל-'0010'.
'F' הופך ל-'1111'.
מחברים: 000100101111 בינארי.
אז '12F' הקסדצימלי = 000100101111 בינארי.

אנחנו לקראת סיום נראה לי... מה עוד? אה! לא דיברנו על פעולות חשבוניות בבסיסים האלו, איך למען השם מסתכלים על כזה דבר?

פעולות חשבוניות בסיסיות:

לצערי, החלק הזה במדריך לא נשמר תוך כדי שלמדתי וערכתי אותו. (ככה"נ המידע נדרס, אירוניה...) אני עובד לשכתב את זה מחדש, אבל החלטתי להעלות בינתיים מה שיש...

חיבור וחיסור:

ספויילר

כפל וחילוק:

ספויילר

מספרים שליליים:

ספויילר

והנה קצת שיעורי בית:
אני אתן לכם כמה שמות של צבעים נפוצים עם הקוד ההקסדצימלי שלהם. המשימה היא להמיר כל קוד צבע הקסדצימלי לקוד צבע בינארי! לא לשכוח, כל סימן הקסדצימלי הופך ל-4 ביטים בינאריים.

הצבעים לאתגר:
אדום - קוד הקסדצימלי: #FF0000
ירוק - קוד הקסדצימלי: #00FF00
כחול - קוד הקסדצימלי: #0000FF
לבן - קוד הקסדצימלי: #FFFFFF
שחור - קוד הקסדצימלי: #000000
אפור - קוד הקסדצימלי: #808080

איך עושים את זה?
לכל צבע, אתה צריך להמיר כל זוג סימנים הקסדצימליים (RR, GG, BB) לבינארי בנפרד.
למשל, עבור צבע אדום (#FF0000):
FF (אדום) -> תמיר את 'F' הראשון לבינארי, ואז את 'F' השני לבינארי, ותחבר אותם.
00 (ירוק) -> תמיר את '0' הראשון לבינארי, ואז את '0' השני לבינארי, ותחבר אותם.
00 (כחול) -> אותו דבר כמו ירוק.
ואז תחברו את שלושת החלקים הבינאריים (אדום, ירוק, כחול) אחד ליד השני, וקיבלתם את קוד הצבע הבינארי!

יאללה, לעבודה! (לא לפסח עדיין, רגע.)

אז, אם הגעתם עד לפה, אשמח גם כאן לשמוע/לקרא הערות/הארות תובנות או הגיגים על כל אחד מהיבטי המדריך הזה (אני לא אתחיל שוב עם הסגנון/וכו'/וכו' כן?) וביחד נהפוך את המדריך הזה לברור ומובן יותר. סגור? בהצלחה.

נ.ב. בבקשה אם אתם רוצים לשתף את המדריך, פשוט תשלחו קישור לכאן, בסדר?

אזולאי

@דאבל אני אוחז רק בשורה הראשונה, שובר את הראש להבין פה משהו,
אבל חייב להגיד זה מדהים, איזה ידע, איזו עוצמה.
זה הזוי להבין דברים כאלה ועוד יותר לכתוב ולפשט את זה, כדי שאנשים פשוטים יבינו...
אני מעריך מאד את כתיבת המדריך הזה, אם לקרוא אותו לוקח זמן, לכתוב אותו בוודא לקח הרבה יותר...
והטירחה למצוא דוגמאות ...
בקיצור תודה רבה

עכשיו אני מבין הרבה יותר את המשפט הקבוע של @המומחים: " אם אני עושה לך עבודה בעשר דקות כנראה למדתי עשר שנים " משהו כזה...

ישצצרר

@אזולאי כתב במדריך | הקסדצימאלי | צעד נוסף להבנת עולם הנתונים:

@המומחים: " אם אני עושה לך עבודה בעשר דקות כנראה למדתי עשר שנים " משהו כזה...

אגב זה מה ש@שמואל כתב בפרופיל שלו
ותודה רבה ל @דאבל היקר שעשה כזה מדריך ניפלא בעיני (אפ' בעיני כולם) כל הכבוד שזכית להנות את כולנו- אשריך!!!!

דאבל

@אזולאי תודה, אם יש שאלות- בשמחה...

יאיר הבהיר

@דאבל היי, מדהים!!
הידע, הכישרון, והכתיבה הכל כך זורמת...

סוף סוף מישהו עוזר להבין מה הולך שם בעולם הטכנולוגי ההזוי הזה

אז רק משהו אחד: רוצים עוד, והרבה!

מיאני ומהשמי

@דאבל מאוד יפה מאוד מושקע ומאוד מובן
ושוב אכתוב כמה שיותר כותרות יותר קל לקרא, ובפרט תוכן עמוק ומסובך בעולם מושגים לא מוכר
ושוב תודה רבה רבה

כמובן שרק בגלל שכתבת כך
@דאבל כתב במדריך | הקסדצימאלי | צעד נוסף להבנת עולם הנתונים:

אז, אם הגעתם עד לפה, אשמח גם כאן לשמוע/לקרא הערות/הארות תובנות או הגיגים על כל אחד מהיבטי המדריך הזה (אני לא אתחיל שוב עם הסגנון/וכו'/וכו' כן?) וביחד נהפוך את המדריך הזה לברור ומובן יותר. סגור? בהצלחה.

הרשתי לעצמי לכתוב ביקורת כי אחרת איזה מקום יש לי מול מי שעושה בשבילי ועוד בכזאת יסודיות

י. פל.

פוסט זה נמחק!

דאבל

@מיאני-ומהשמי שוב תודה על ההערה, אני באמת מחכה לזה. (כשאני בתוך הלמידה אני משתדל לכתוב יותר בצורה של שיעור ופחות מדריך...
אבל תוך כדי זה נראה לי מספיק ברור, כי אני לומד כל חלק בנפרד עד שזה מצטבר לכזה אורך...)
@י-פל תודה על ההערה, לפי הידוע לי, צריך להצהיר שמדובר במספר הקסדצימאלי אחרת הוא יבין שזה מספר עשרוני או משתנה שהוא לא מכיר.. אם כי אפשר להשתמש בפונקציה hex() או להגדיר בint בסיס 16 כארגומנט השני ואז לא צריך לכתוב קידומת למספר. (זכור לי שקראתי על עוד אפשרויות, לא זוכר כרגע...)

י. פל.

פוסט זה נמחק!

דאבל

חברים, סיימתי להשלים גם את הקטע של פעולות חשבוניות אבל הוא יצא יותר ארוך מכל המדריך...
מה אתם אומרים, יש עניין להעלות הכל? אולי רק ממש את הבסיס? יהיה מישהו שישב ללמוד מתמטיקה?

משחזר מידע

@דאבל כתב במדריך | הקסדצימאלי | צעד נוסף להבנת עולם הנתונים:

יהיה מישהו שישב ללמוד מתמטיקה?

בעולם של היום שהאשכולות הכי מפוצצות הם כל מה שקשור לAI
נראה לך שמישהו ישקיע תזמן לזה
לאף אחד היום לא מעניין ידע
רוצים תוצאות עכשיו ומיד

משתתף בצערך על הזמן שבזבזת

דאבל

@משחזר-מידע תודה, אבל לא בזבזתי זמן, אני נהנה ללמוד...
אבל כנראה שאתה צודק

אזולאי

@דאבל כתב במדריך | הקסדצימאלי | צעד נוסף להבנת עולם הנתונים:

תודה, אבל לא בזבזתי זמן, אני נהנה ללמוד...
אבל כנראה שאתה צודק

יתכן שלא יקראו את זה הרבה אנשים, אבל אם אתה רוצה לדעת אני כן, ואני בטוח שיש עוד כמוני.
אני טיפוס שאוהב ידע ומשקיע הרבה בשביל להבין מה עומד לפני....

@משחזר-מידע , אתה כותב מהניסיון שלך, אבל עדיין יש אנשים שלומדים ומשקיעים.

משחזר מידע

@אזולאי כתב במדריך | הקסדצימאלי | צעד נוסף להבנת עולם הנתונים:

אבל עדיין יש אנשים שלומדים ומשקיעים.

אלה לא נמצאים כאן בפורום
הם יושבים ולומדים

יאיר הבהיר

@דאבל
@אזולאי כתב במדריך | הקסדצימאלי | צעד נוסף להבנת עולם הנתונים:

יתכן שלא יקראו את זה הרבה אנשים, אבל אם אתה רוצה לדעת אני כן, ואני בטוח שיש עוד כמוני.
אני טיפוס שאוהב ידע ומשקיע הרבה בשביל להבין מה עומד לפני....

מצטרף... [אולי תפתח את זה בפוסט חדש]

דאבל

@יאיר-הבהיר לא רואה עניין לפתוח נושא חדש, זה הרחבה של אותו עניין...
בכ"א אני חושב לעצור איפה שהספקתי לכתוב עד עכשיו, נראה לי מספיק, אם יהיה דרישה אולי נמשיך...
אני מקווה להספיק לערוך היום את הפוסט ולהכניס חלק...

מוטי זהב

קודם כל תודה על ההסבר הפשוט בעניין הקסדימאלי חידשת לי

@דאבל כתב במדריך | הקסדצימאלי | צעד נוסף להבנת עולם הנתונים:

חיבור וחיסור:

לכאורה פשוט מאוד
חיבור כמו תרגיל חשבון פשוט מימין לשמאל כאשר כל 16 שנצברים עוברים ל"מחסן" בשביל התרגיל הבא
חיסור כנ"ל רק כאשר לוקחים "השאלות" המספירם נהיים ל16
כפל ג"כ כמו כפל רגיל (מדרגות, את התוצאה מחלקים ל16 ושמים ב"מחסן" לתרגיל הבא ואז עושים תרגיל חיבור בין כל התוצאות בכל המדרגות)
בקיצור זה רק לשנות את הראש ולחשוב בצורה "שישישרונית" במקום עשרונית
(אפשר גם לעשות המרה הלוך חזור הקסדמצימאלי לעשרוני לעשות חישוב ולהחזיר
אבל לדעתי זה משנה כמו שאני יפתח נושא עכשיו על כפל בשברים פשוטים
ולהסביר ש1/4 לחלק ל1/2 שוה 1/2 ו1/2 לחלק ל1/4 שווה 2

דאבל

@מוטי-זהב בעצם הסיכום שלך נכון, הרוב זה אותו עיקרון כמו בעשרוני, אבל לא זוכר אם כבר כתבתי, כל המדריך שכתבתי אפשר לכתוב הרבה יותר קצר, העניין הוא שאני כותב את זה כשיעור, שכולל גם תרגול ולא רק את העקרונות...
מה שאומר שלמשל כפל וחילוק הרבה יותר קל כמו שאתה אומר להמיר לעשרוני, לעשות את הפעולה ולהמיר חזרה.
ושוב, המדריך הוא על הקסדצימאלי ולא על מתמטיקה, אבל כל זה מחדד ומעשיר את הידע...
וחוץ מזה יש את שאר הנושאים שעובדים אחרת לגמרי. כמו למשל המספרים השליליים, מספרים לא שלמים...

מוטי זהב

@דאבל כתב במדריך | הקסדצימאלי | צעד נוסף להבנת עולם הנתונים:

וחוץ מזה יש את שאר הנושאים שעובדים אחרת לגמרי. כמו למשל המספרים השליליים, מספרים לא שלמים...

מחכה לזה
אבל כמובן להבין את הרעיון ולא נוסחאות\תבניות

userbot

א. תודה רבה על המדריך המושקע!!
אשמח מאד אם יהיה מדריך או פירוט על מה אפשר לעשות עם זה
כי בסוף את החישוב אפשר לעשות עם עזרים שונים (AI ..)
אבל מה בדיוק אפשר לעשות עם זה, זה קשור יותר למבנה מערכת הקבצים
אשמח שתרים את הכפפה גם לזה זה יעזור מאד!

מעניין אותי יותר הקטע של שיחזור נתונים וכו' אבל כל מידע יעזור